Difference Between Tree And Graph

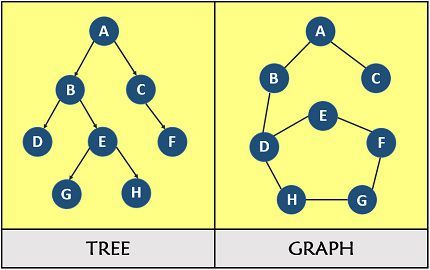Tree vs graph Tree and graph come up under the category of non-linear data structure where tree offers a very useful way of representing a relationship betwixt the nodes in a hierarchical structure and graph follows a network model. Tree and graph are differentiated by the fact that a tree structure must be connected and can never have loops while in the graph there are no such restrictions.

A non-linear data structure consists of a drove of the elements that are distributed on a plane which means there is no such sequence between the elements as it exists in a linear data structure.

Content: Tree Vs Graph

1. Comparison Chart
2. Definition
3. Key Differences
4. Decision

Comparing Nautical chart

Footing for comparing	Tree	Graph
Path	Just one between two vertices.	More than ane path is allowed.
Root node	It has exactly one root node.	Graph doesn't take a root node.
Loops	No loops are permitted.	Graph can have loops.
Complexity	Less complex	More circuitous comparatively
Traversal techniques	Pre-social club, In-order and Post-order.	Breadth-outset search and depth-first search.
Number of edges	northward-1 (where n is the number of nodes)	Non defined
Model blazon	Hierarchical	Network

Definition of Tree

A tree is a finite collection of data items ordinarily termed as nodes. Every bit information technology is mentioned above that a tree is a non-linear data structure which arranges data items in sorted social club. Information technology is used to prove a hierarchical structure between the various data elements and organizes the data into branches which relate the information. The improver of a new edge in a tree results in a formation of the loop or circuit.

There are several types of trees such as a binary tree, binary search tree, AVL tree, threaded binary tree, B-tree, etc. Information compression, file storage, manipulation of the arithmetics expression and game copse are some of the application of tree data construction.

Properties of tree:

In that location is designated node at the acme of the tree known as a root of the tree.
The remaining data items are divided into disjoint subsets refer to equally subtree.
The tree is expanded in height towards the bottom.
A tree must be connected which ways in that location must exist a path from i root to all other nodes.
It does not contain any loops.
A tree has n-ane edges.

There are various terms associated with trees such as concluding node, border, level, degree, depth, forest, etc. Among those terms, some of them described below.

Border – A line which connects 2 nodes.
Level – A tree is partitioned into levels such a way that the root node is at level 0. And so, its firsthand children are at level i, and its immediate children are at level ii and and then on upwardly to the concluding or leaf node.
Caste – It is the number of subtrees of a node in a given tree.
Depth – It is the maximum level of any node in a given tree and too known as height.
Terminal node – The highest level node is terminal node while other nodes except final and root node are known as not-final nodes.

Definition of Graph

A graph is also a mathematical non-linear data construction which tin can correspond various kinds of physical construction. It consists of a group of vertices (or nodes) and prepare of edges that connect the two vertices. Vertices on the graph is represented equally point or circles and edges are shown as arcs or line segments. An border is represented by Due east(5,due west) where v and westward are the pairs of vertices. Removal of an edge from a circuit or connected graph creates a subgraph that is a tree.

The graphs are classified into various categories such every bit directed, non-directed, continued, not-connected, elementary and multi-graph. Figurer network, transportation organization, social network graph, electrical circuits and project planning are some of the applications of graph data construction. It is besides employed in management technique named as PERT (program evaluation and review technique) and CPM (disquisitional path method) in which the graph structure is analysed.

Properties of a graph:

A vertex in a graph tin be connected to any number of other vertices using edges.
An edge tin can exist bidirected or directed.
An edge can be weighted.

In graph too we use various terms like adjacent vertices, path, cycle, degree, continued graph, complete graph, weighted graph, etc. Let's understand some of these terms.

Adjacent vertices – A vertex a is next to vertex b if in that location is an edge (a,b) or (b,a).
Path – A path from a random vertex due west is an adjacent sequence of vertices.
Bike – It is a path where the first and last vertices are the same.
Caste – It is a number of edges incident on a vertex.
Continued graph – If there exists a path from a random vertex to any other vertex, then that graph is known equally a connected graph.

Fundamental Differences Between Tree and Graph

In a tree there be only one path between whatsoever ii vertices whereas a graph can have unidirectional and bidirectional paths between the nodes.
In the tree, there is exactly one root node, and every child can accept only one parent. As against, in a graph, there is no concept of the root node.
A tree tin not have loops and self-loops while graph can have loops and self-loops.
Graphs are more complicated as it tin can have loops and self-loops. In dissimilarity, trees are simple as compared to the graph.
The tree is traversed using pre-order, in-lodge and post-order techniques. On the other hand, for graph traversal, nosotros use BFS (Breadth First Search) and DFS (Depth Get-go Search).
A tree can have n-1 edges. On the contrary, in the graph, there is no predefined number of edges, and it depends on the graph.
A tree has a hierarchical construction whereas graph has a network model.

Decision

Graph and tree are the not-linear data structure which is used to solve various circuitous problems. A graph is a group of vertices and edges where an edge connects a pair of vertices whereas a tree is considered as a minimally connected graph which must exist continued and free from loops.