Linear Equations In Three Variables

Learning Outcomes

Solve systems of iii equations in three variables.
Identify inconsistent systems of equations containing 3 variables.
Express the solution of a system of dependent equations containing 3 variables using standard notations.

John received an inheritance of $12,000 that he divided into iii parts and invested in three ways: in a money-market place fund paying 3% annual involvement; in municipal bonds paying four% annual interest; and in mutual funds paying 7% almanac interest. John invested $4,000 more in municipal funds than in municipal bonds. He earned $670 in involvement the first year. How much did John invest in each type of fund?

A pile of quarters, dimes, nickels, and pennies.

(credit: "Elembis," Wikimedia Commons)

Agreement the right arroyo to setting upwards problems such as this i makes finding a solution a matter of following a design. Nosotros will solve this and like problems involving iii equations and iii variables in this section. Doing then uses similar techniques as those used to solve systems of two equations in two variables. Nevertheless, finding solutions to systems of three equations requires a bit more arrangement and a touch of visual gymnastics.

Solve Systems of Three Equations in Iii Variables

In gild to solve systems of equations in iii variables, known as three-past-three systems, the primary goal is to eliminate ane variable at a time to accomplish dorsum-substitution. A solution to a arrangement of three equations in three variables [latex]\left(x,y,z\right),\text{}[/latex] is called an ordered triple.

To find a solution, we tin perform the following operations:

Interchange the order of any two equations.
Multiply both sides of an equation past a nonzero constant.
Add a nonzero multiple of one equation to another equation.

Graphically, the ordered triple defines the point that is the intersection of three planes in space. You tin can visualize such an intersection by imagining whatever corner in a rectangular room. A corner is divers by 3 planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor come across represents the intersection of three planes.

A General Annotation: Number of Possible Solutions

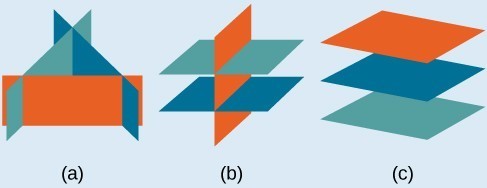
The planes illustrate possible solution scenarios for three-by-three systems.

Systems that take a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of 3 planes in space.
Systems that take an infinite number of solutions are those which, after emptying, result in an expression that is always truthful, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or ancillary plane that serves as the intersection of three planes in space.
Systems that take no solution are those that, subsequently emptying, event in a statement that is a contradiction, such as [latex]three=0[/latex]. Graphically, a system with no solution is represented by iii planes with no point in common.

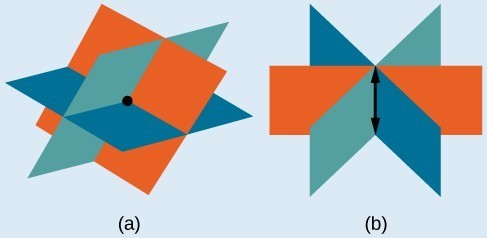
(a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) 3 planes intersect in a line, representing a three-by-iii system with infinite solutions.

Example: Determining Whether an Ordered Triple Is a Solution to a System

Determine whether the ordered triple [latex]\left(three,-2,1\right)[/latex] is a solution to the system.

[latex]\begin{gathered}x+y+z=2 \\ 6x - 4y+5z=31 \\ 5x+2y+2z=13 \finish{gathered}[/latex]

How To: Given a linear organisation of three equations, solve for 3 unknowns.

Pick any pair of equations and solve for one variable.
Pick another pair of equations and solve for the same variable.
You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
Back-substitute known variables into whatever one of the original equations and solve for the missing variable.

Example: Solving a Arrangement of Three Equations in Three Variables by Elimination

Find a solution to the post-obit system:

[latex]\begin{align}x - 2y+3z=9& &\text{(one)} \\ -x+3y-z=-6& &\text{(ii)} \\ 2x - 5y+5z=17& &\text{(iii)} \cease{align}[/latex]

Try It

Solve the organization of equations in 3 variables.

[latex]\begin{array}{l}2x+y - 2z=-1\hfill \\ 3x - 3y-z=5\hfill \\ x - 2y+3z=six\hfill \stop{array}[/latex]

Evidence Solution

[latex]\left(i,-1,ane\right)[/latex]

In the following video, you will see a visual representation of the three possible outcomes for solutions to a system of equations in three variables. There is also a worked example of solving a system using elimination.

Example: Solving a Existent-Globe Trouble Using a System of Three Equations in Three Variables

In the problem posed at the beginning of the section, John invested his inheritance of $12,000 in three dissimilar funds: role in a money-market fund paying iii% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying seven% annually. John invested $4,000 more in common funds than he invested in municipal bonds. The total interest earned in one twelvemonth was $670. How much did he invest in each blazon of fund?

Attempt It

Classify Solutions to Systems in Three Variables

Just equally with systems of equations in ii variables, we may come across an inconsistent system of equations in three variables, which means that it does non have a solution that satisfies all three equations. The equations could correspond three parallel planes, two parallel planes and ane intersecting aeroplane, or three planes that intersect the other two but non at the same location. The process of elimination will result in a false statement, such equally [latex]3=7[/latex] or some other contradiction.

Case: Solving an Inconsistent System of Three Equations in 3 Variables

Solve the following arrangement.

[latex]\brainstorm{marshal}x - 3y+z=4 && \left(1\right) \\ -x+2y - 5z=3 && \left(2\right) \\ 5x - 13y+13z=viii && \left(3\right) \terminate{align}[/latex]

Try It

Solve the system of three equations in iii variables.

[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ \text{ }y - 3z=ane\hfill \\ 2x+y+5z=0\hfill \cease{array}[/latex]

Show Solution

No solution.

Expressing the Solution of a System of Dependent Equations Containing Three Variables

Nosotros know from working with systems of equations in ii variables that a dependent organisation of equations has an infinite number of solutions. The same is true for dependent systems of equations in three variables. An infinite number of solutions can result from several situations. The three planes could be the aforementioned, and so that a solution to one equation will be the solution to the other ii equations. All three equations could be different but they intersect on a line, which has infinite solutions. Or 2 of the equations could be the same and intersect the 3rd on a line.

Example: Finding the Solution to a Dependent System of Equations

Find the solution to the given organization of iii equations in 3 variables.

[latex]\brainstorm{align}2x+y - 3z=0 && \left(ane\right)\\ 4x+2y - 6z=0 && \left(two\right)\\ x-y+z=0 && \left(iii\right)\end{align}[/latex]

Q & A

Does the generic solution to a dependent organisation ever accept to be written in terms of [latex]10?[/latex]

No, you can write the generic solution in terms of any of the variables, but information technology is mutual to write it in terms of [latex]10[/latex] and if needed [latex]x[/latex] and [latex]y[/latex].

Try Information technology

Solve the following system.

[latex]\begin{gathered}10+y+z=7 \\ 3x - 2y-z=4 \\ x+6y+5z=24 \end{gathered}[/latex]

Evidence Solution

Infinitely many number of solutions of the form [latex]\left(ten,4x - 11,-5x+18\right)[/latex].

Central Concepts

A solution prepare is an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex] that represents the intersection of 3 planes in space.
A arrangement of three equations in 3 variables can exist solved by using a series of steps that forces a variable to be eliminated. The steps include interchanging the gild of equations, multiplying both sides of an equation by a nonzero abiding, and adding a nonzero multiple of one equation to another equation.
Systems of three equations in iii variables are useful for solving many different types of existent-earth problems.
A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the consequence is a contradiction.
Systems of equations in iii variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other ii but not at the same location.
A arrangement of equations in iii variables is dependent if it has an infinite number of solutions. After performing elimination operations, the result is an identity.
Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or ii identical planes that intersect the third on a line.

Glossary

solution set the set up of all ordered pairs or triples that satisfy all equations in a system of equations