How To Calculate Rectangular Prism

In geometry, arectangular prism is a polyhedron with two congruent and parallel bases. It is too called a cuboid. A rectangular prism has half dozen faces, and all the faces are in a rectangle shape and have twelve edges. Because of its cantankerous-department along the length, it is said to be a prism. Geometry is the written report of shapes and the configuration of objects. Similar to other three-dimensional shapes, a rectangular prism also has its area and book. The surface surface area of the prism is the area of its net. In this article, let us discuss the definition, types, surface area, and volume of a rectangular prism in detail.

What is a Rectangular Prism?

A rectangular prism is a three-dimensional shape, that has six faces (2 at the top and bottom and four are lateral faces). All the faces of the prism are rectangular in shape. Hence, there are three pairs of identical faces here. Due to its shape, a rectangular prism is also called a cuboid. Some of the real-life examples of a rectangular prism are a geometry box, notebooks, diaries, rooms, etc. In the below figure, nosotros can encounter the shape of a rectangular prism.

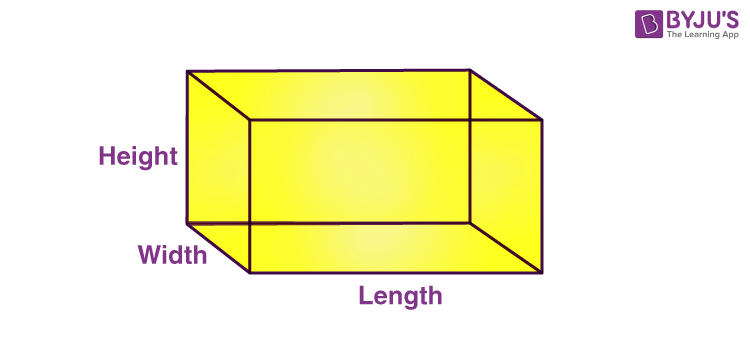
Rectangular pyramid

Properties of Rectangular Prism

A rectangular prism has 6 faces, 12 edges and 8 vertices
The superlative and base of the rectangular prism are ever a rectangle
Like cuboid, it also has three dimensions, i.east., length width and height
Pairs of contrary faces are identical or coinciding
For a right rectangular prism, the lateral faces are rectangle
For an oblique rectangular prims, the lateral faces are parallelogram
Information technology has a rectangular cross-section
It looks exactly like a cuboid

Types of Rectangular Prism

Rectangular prism can be classified into ii different types. They are:

Right Rectangular Prism
Oblique Rectangular Prism

Correct Rectangular Prism

A prism with rectangular bases is called a rectangular prism. A correct rectangular prism is a prism that has six faces that are rectangles, and all angles are right angles.

Vertices of a rectangular prism = 8
Edges of a rectangular prism = 12
Faces of a rectangular prism= half-dozen (including bases)

Oblique Rectangular prism

An oblique prism is a prism in which the bases are not perpendicular to each other. A rectangular prism with bases that are not aligned one straight above the other is an oblique rectangular prism.

Types of rectangular prism

Rectangular Prism Formulas

A rectangular prism is a 3-dimensional object. Hence, it will take its surface area and book. To calculate the volume and surface surface area of a prism, we accept to know the length of its sides or edges. Allow 'fifty', 'w' and 'h' be the length, width and top of the rectangular prism. The formulas are given below.

Volume of a Rectangular Prism Formula

The volume of a rectangular prism is a measurement of the occupied units of a rectangular prism. The volume of a rectangular prism is represented by cubic units. It is also defined every bit the number of units used to fill a rectangular prism.

The volume of the rectangular prism is equal to the area of the base times its height.

Therefore, the volume of a rectangular prism formula is given every bit

The volume of a rectangular prism = Length ten Width 10 Height cubic units.

Volume = fifty x w x h cubic units

Surface Expanse of a Rectangular Prism

The surface area of a rectangular prism is the measure out of how much-exposed area a prism has. Expanse is expressed in square units. The total surface area of a rectangular prism is the sum of the lateral surface area (LSA) and twice the base area of the rectangular prism.

Total Surface Area of rectangular prism = LSA + two (Base of operations expanse) [Square units]

The lateral surface area of a rectangular prism is the sum of the surface area of all its faces without the base of the rectangular prism. The lateral expanse of any right rectangular prism is equivalent to the perimeter of the base of operations times the height of the prism.

Therefore, the lateral surface expanse = P x h [Square units]

Where

P is the perimeter of a base

h be the acme of the prism

The perimeter of the rectangular prism is,

Therefore, the lateral surface expanse (LSA) of a rectangular prism = ii ( 50 + w ) h foursquare units.

Hence,

TSA = LSA + 2 (Base Area) = ii (l + w) h + ii (l x w) = 2 lh + 2 wh + 2 lw [Square units]

Therefore, the surface area of a rectangular prism formula is given as,

Surface Area of a rectangular prism = 2 (lh +wh + lw ) Square units.

Rectangular Prism Net

The internet of any prism is its surface expanse. Information technology shows when nosotros open the prism in a plane; then all its sides could be visible at the aforementioned fourth dimension. If we calculate the private area of all its sides using the internet, we will get the total surface area. See the figure below to find the net for the rectangular prism.

Net of rectangular prism

You tin can see from the above figure, all the sides of the prism are in a rectangular shape. By using the formula for the surface area of rectangle, you can notice the areas for each face and add all the areas to get the net of the prism.

Prism
Rectangular Pyramid
Area of Rectangle
Pentagonal Prism
Square prism
Triangular Prism
Volume of a Prism

Solved Examples on Rectangular Prism

Question 1: Find the volume of a rectangular prism whose length, width, and height are 8cm, 6cm, and 4cm, respectively.

Solution:

Given:

Length, fifty = eight cm

Width, w = 6 cm

Pinnacle, h = iv cm

The formula to notice the volume of a rectangular prism is,

V = Length x Width x Elevation cubic units

5 = viii x 6 10 iv cm^three

V = 192 cm^three

Therefore, the volume of a rectangular prism is 192 cm³.

Question 2: Find the area of a rectangular prism whose length, width, and height are 8cm, 6cm, and 4cm, respectively.

Solution: Given:

Length, l = viii cm

Width, w = 6 cm

Summit, h = 4 cm

The formula to find the surface area of a rectangular prism is,

A = two (lh +wh + lw )

A = 2 (8×4+6×4+8×half dozen)

A = ii(32+24+48)

A = 2(104)

A = 208 sq.cm.

Practice Questions

1. Find the area of a rectangular prism whose length, width, and height are given, respectively.

3cm, 4cm and 5cm
ii.five cm, 6cm, 9cm
five cm, 8cm, 10cm
6.2 cm, 4.4 cm, 9cm

2. Find the book of rectangular prism with the post-obit dimensions.

3cm x 4cm x 5cm
2.5 cm x 6cm 10 9cm
5 cm x 8cm x 10cm
vi.2 cm x 4.4 cm x 9cm

Stay tuned with BYJU'S – The Learning App for more Maths-related concepts and download the app to watch personalized videos.

Frequently Asked Questions on Rectangular Prism

What is the correct rectangular prism?

A right rectangular prism has half dozen rectangular faces, 12 edges and viii vertices. It is too called a cuboid.

What is the departure between the right rectangular prism and an oblique rectangular prism?

The bases of the right rectangular prism are perpendicular to each other whereas the bases of the oblique rectangular prism are not perpendicular.

What is an example of a rectangular prism?

The rectangular prism examples in real life are bricks, books, doors, etc.

What is the volume of a rectangular prism?

The volume of a rectangular prism is equal to the product of its length, width and height.

What is the expanse of a rectangular prism?

The expanse of a rectangular prism is given by:
SA = 2 (lh +wh + lw ) Square units.

What is the rule for rectangular prism?

The bases of rectangular prism (top and bottom) should be rectangular in shape.

Is a rectangular prism also a cuboid?

A right rectangular prism has all its half dozen faces, rectangular, similar to a cuboid. Hence it is also known as a cuboid.